Understanding algorithms and the techniques you can use to solve them, is crucial for any junior developer. Whether you are prepping for an upcoming job interview or trying to improve your problem solving skills, these patterns or techniques can help you succeed. This is part two of a four part series where I will explore different patterns used to solve common algorithm challenges (check out part one on the multiple pointers pattern). As someone who despised algorithms during my bootcamp, this series is mainly an effort to document my learning, overcome my dislike towards algorithms, and become a better problem solver. I hope you’ll join me on this journey!
Let’s get started! ✈️
What is the Sliding Window Technique?
The sliding window technique essentially involves creating a window which can either be an array or number that “slides” from one position to another. Depending on a certain condition, the window will either increase or close (creating a new window). This technique is useful for keeping track of a subset of contiguous data in an array or string. Common examples of when you might use this technique include finding the longest sequence of unique characters, calculating the max sum of consecutive elements in an array, and much more.
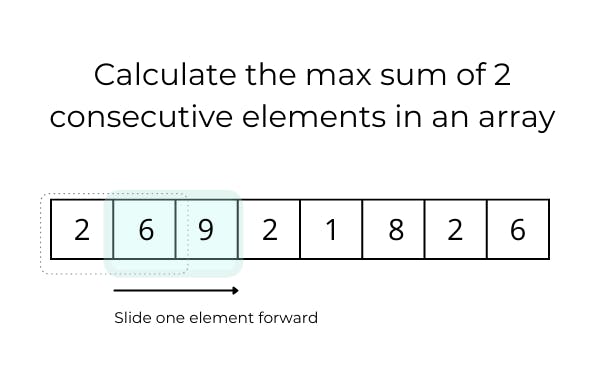
In the example above, the window will keep sliding through the array by one element until the max sum of 2 consecutive elements is found (in this case, 15). Keep in mind that in different problems the window size can either remain constant or grow or shrink.
The main benefit of using the sliding window technique is time complexity. Instead of using a nested for loop, a single loop can be used to reduce the time complexity ideally resulting in O(n) time complexity.
Let’s dive into an example problem to better understand this technique.
Example Problem 1 - Max Subarray Sum
Problem: Calculate the max sum of n consecutive elements in an array.
Input: [2, 6, 9, 2, 1, 8, 2, 6], 2
Expected Output: 15
Let’s try out the sliding window technique to solve this! We are going to need a variable to store the max sum, and a variable to store the temporary sum that we use while we loop through the array. Let’s also add an edge case for arrays that have a length smaller than n.
const maxSubarraySum = (arr, n) => {
let maxSum = 0;
let tempSum = 0;
if (arr.length < n) return null;
}
Now, we need to make our window. For now, we are going to add n digits of our array to find the sum of the first n digits and assign it to tempSum.
const maxSubarraySum = (arr, n) => {
let maxSum = 0;
let tempSum = 0;
if (arr.length < n) return null;
for (let i = 0; i < n; i++) {
maxSum += arr[i];
}
tempSum = maxSum;
}
We are going to create another for loop, but this loop is going to start at index n. We already have the sum of the first n indexes so let’s start sliding our window. To do this we will need to add the next number to tempSum and subtract the first number in our window.
The original array:
[2, 6, 9, 2, 1, 8, 2, 6]
Our current window:
[2, 6]
Our window after one iteration:
[6, 9]
After a second iteration:
[9,2]
The last step is to just compare maxSum and tempSum with Math.max to find the larger value.
//Calculate the max sum of n consecutive elements in the array
const maxSubarraySum = (arr, n) => {
let maxSum = 0;
let tempSum = 0;
if (arr.length < n) return null;
for (let i = 0; i < n; i++) {
maxSum += arr[i];
}
tempSum = maxSum;
for (let i = n; i < arr.length; i++) {
tempSum = tempSum - arr[i - n] + arr[i];
maxSum = Math.max(maxSum, tempSum);
}
console.log(maxSum)
}
maxSubarraySum([2, 6, 9, 2, 1, 8, 2, 6], 2) // 15
Example Problem 2 - Find Duplicates Within a Range
Problem: Given an array and a positive number k, check whether the array contains any duplicate elements within the range k. If k is more than the array’s size, the solution should check for duplicates in the complete array. Return true and the repeated number or return false if there are no duplicates.
Input: [1, 2, 3, 4, 5, 6, 7, 5], 4
Expected Output: True, the first repeated number is 5
Similar to the other example, we are going to create our window first and a for loop. The first condition in that for loop is going to check if the window includes the current index. If it does return true, because there is a duplicate.
const findDuplicatesWithinRange = (arr, k) => {
let window = [];
for (let i = 0; i < arr.length; i++) {
if (window.includes(arr[i])) {
return `true, the first repeated number is ${arr[i]}`
}
}
return false
}
If the number is not in our window, then we need to push it in. But we can’t just push all the elements into the window. We need to add a conditional for if i >= k we remove the first index and continue moving through the array.
const findDuplicatesWithinRange = (arr, k) => {
let window = [];
for (let i = 0; i < arr.length; i++) {
if (window.includes(arr[i])) {
return `true, the first repeated number is ${arr[i]}`
}
window.push(arr[i])
if (i >= k) {
window.shift()
}
}
return false
}
console.log(findDuplicatesWithinRange([1, 2, 3, 4, 5, 6, 7, 5], 4)) // "True, the repeated number was 5"
This approach is very similar to the first solution except that we do not create the window first before iterating through the array and making comparisons.
Conclusion
It’s still hard for me to find the motivation to practice algorithms and then write about them (hence, why there is such a big gap between part one and part two of this series). I’d much rather work on a fun side project or explore a new language or framework, but learning and writing about these patterns has already helped my approach towards problems tremendously. I hope to continue to build my problem solving toolkit and train my brain to become a better problem solver.
Thanks for reading!! 🦋

