Algorithm Patterns - Multiple Pointers

I’ll admit that I have an issue. I hate algorithms and I’m not very good at them. And the latter may be influencing my hatred towards them. During my bootcamp’s “Algo Fridays” I would mostly curl up into a ball and admit defeat. Claiming “I’m just not good at this” or “I won’t need algos for front-end development”. But I’m on a mission to improve my algorithm skills by learning patterns, knowing when to use them, and implementing those patterns. My goal is that by learning and practicing these patterns I will become a better problem solver.

This will be part one of a four part series. In each article I’ll do a deep dive into an algorithm pattern, solve some problems, and hold myself accountable by treating this as a journal of sorts. I welcome anyone trying to improve their algorithm skills to join me.

What is the Multiple Pointers Pattern?

The first pattern I will be exploring is the Multiple Pointers Pattern. I learned of this pattern through a great Udemy course about JS Algorithms and Data Structures that I highly recommend (I’ll get through it all one day I swear 😅). This pattern involves creating pointers or values that typically correspond to an index in an array. Those pointers then move towards the beginning, middle, or end based on the condition. The pointers will continue to move until a pair or the desired goal is reached. This is demonstrated in the diagram below. Using the multiple pointers pattern, the returned value in this example would be [-3, 3].

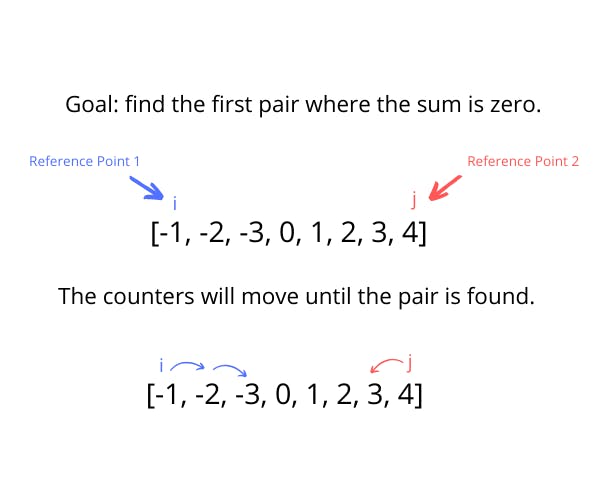
To understand this pattern more, let’s see it in action with an example problem.

Example Problem 1 - Find the Runner-Up Score

You are given a score sheet and are required to find the runner-up score. You will be given the scores as in an array like so:

Input: [2, 3, 6, 6, 5, 6, 6, 2, -22]

Expected Output: 5

Let’s use the multiple pointers pattern to solve this. We'll start by making sure the array length is greater than 0 and sorting our array in descending order to make our lives easier.

const findTheRunnerUp = (arr) => {
    if (arr.length === 0) {
        return;
    }
    arr = arr.sort((a, b) => b - a);
}

Now let’s create our first pointer. This will start at index 0 and be incremented only if arr[i] is equal to our second pointer. Let’s declare that runnerUp variable that we’ll return as well.

const findTheRunnerUp = (arr) => {
    if (arr.length === 0) {
        return;
    }
    arr = arr.sort((a, b) => b - a);
    let i = 0;
    let runnerUp; 
}

To get our second pointer, we will create a for loop with j, our pointer, set to index 1. While we loop through the array, we will compare arr[i] toarr[j]` to find out if they are equal to each other. If they are, we will increment and skip that number. If not, since our array is already sorted, we know that the number at that index is our runner-up.

const findTheRunnerUp = (arr) => {
    if (arr.length === 0) {
        return;
    }
    arr = arr.sort((a, b) => b - a);
    let i = 0;
    let runnerUp;
    for(let j = 1; j < arr.length; j++) {
        if (arr[i] !== arr[j]) {
            runnerUp = arr[j]
            return runnerUp;
        } else {
            i++;
        }
    }
}
let array = [2, 3, 6, 6, 5, 6, 6, 2, -22];
console.log(findTheRunnerUp(array))
// Output: 5

Play with the JSFiddle.

This pattern has been working great for me, because visually, it is easy to think of variable i starting at index 0 (in this case number 6) and variable j starting at index 1 (also 6 in this case) and moving through the array until i = 6 and j = 5.

Let’s move onto another example.

Example Problem 2 - Two Sum Sorted

In the previous example, both pointers were moving in the same direction. For this problem, we are going to have our pointers moving in opposite directions.

The Problem: Given an array of integers nums and an integer target, return the two integers that add up to target. Only one valid answer exists and you may assume that each input would have exactly one solution, and you may not use the same element twice.

Input: nums = [1, 4, 5, 6, 10], target = 9;

Output: [4, 5]

Let’s dive into the problem. To begin, declare two variables, one that starts at the beginning of the array and another at the end. We will also need a variable to hold the sum. Think about the goal of this problem, how might we work with these two indexes to find numbers that reach our target? Let’s start with what we know and just declare what we want to happen if the sum of our two pointers is the target.

const twoSumSorted = (nums, target) => {
  let left = 0;
  let right = nums.length - 1;
  let sum = 0;
  while (left < right) {
    sum = nums[left] + nums[right];
  }
}

Now all we have to do is figure out what to do if the sum is not equal to our target. Basically, if the sum ends up being greater than our target, we will want to decrement our right variable. Because there's only one solution per the definition of the problem, we’re safe to keep moving on with our pointer. To cover instances for when the sum is greater than the target we’ll just increment the left variable. And that’s it!

const twoSumSorted = (nums, target) => {
  let left = 0;
  let right = nums.length - 1;
  let sum = 0;
  while (left < right) {
    sum = nums[left] + nums[right];
    if (sum === target) {
      return [nums[left], nums[right]];
    } else if (sum > target) {
      right--;
    } else {
      left++;
    }
  }
};
// Input: [1, 4, 7, 8, 9 ,10], 12
// Output:  [4, 8]

Play with the JSFiddle.

Conclusion

As annoying as the truth is, the only way to get better at something is to practice and that goes for the things you hate as well. I hope that this series and learning more patterns will change how I feel towards algorithms. And if not, at least I’ll be better than when I started.